 People saying 2 + 2 = we can't know.
People saying 2 + 2 = we can't know.
2 + 2 never equals 5
The Weimarization of truth and knowledge at the hands of critical social justice. A mirror of current news articles and threads.
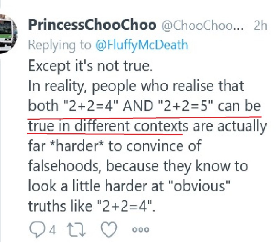
The above is a screenshot of people saying 2+2=5. You read that right...2+2=5. Among them are teachers, educators, and professors who plan on teaching this stuff to your children. So let's talk about what's going on here, why they're doing this, and how we can stop it.
To start, lets look at exactly what they say as how they argue here is very important. They don't say 2+2=4 is false. They don't say 2+2 always equals 5. What they say is: A. 2+2 can sometimes equal 5, And B. That 2+2 doesn't always equal 4.
Please read that again carefully.
Please notice the woke are not arguing that 2+2 always equals 5, nor do they argue that 2+2 never equals 4. The woke think there is no universally correct answer to 2+2 that is objectively true in all situations. They aren't falsifying 2+2=4, they are deconstructing it.
How does deconstruction work? Deconstruction works by attacking at the level of meaning. This means that words, ideas, concepts, discourses, art, texts, symbols; whatever is used to mean something or communicate gets deconstructed. Thus deconstruction "destabilizes meaning."
Wokies destabilize meaning because when a things meaning is not stable, clear, and defined the meaning of the thing can be redefined and distorted. Then people can come to any conclusion they want about it. Here are examples from art, architecture and international relations.
Woke people think racism, sexism, and bigotry are baked into the language and concepts we use. Since we think and communicate with language, if the language we use is inherently racist and sexist then our communication, and the ideas we communicate will be racist and sexist...
This extends into Math. The woke argue objectivity and any either/or binary about truth (answers are either true or false) are part of white supremacy. Since math uses objectivity and thinks things can be either true or false, math is rooted in white supremacy. Take a look.


“Freedom is the freedom to say that 2+2=4. If that is granted, all else follows” -George Orwell, Nineteen Eighty-four
Occasionally in the course of human events it becomes necessary to have explain something no one would ever have expected to have to defend. In the present moment, we find that circumstance to be the case and that thing to be that two and two do, in fact, make four. Further, it must be reasserted, against all reasonable expectation, that this claim about the sum of two and two being four is not merely some subjective determination or, more insidiously, an assertion of hegemonic power. So it is that such a need might arise in such a time in which irrational subjectivity becomes so desperate to defend and assert itself that no truth, no matter how simple or basic, can be considered safe from the ravages of people who have a vested ideological interest in its being wrong.
I have to confess responsibility for this bizarre moment, which in some sense might be one of the greater achievements of my life thus far. There’s an excellent case to be made that I have led a significant number of professionals who definitely should know otherwise—as effectively every six-year-old in a community with a school does—to dig deeply into tortured defenses of the proposition that two and two do not make four.
What in the World…?
“He wondered, as he had many times wondered before, whether he himself was a lunatic. Perhaps a lunatic was simply a minority of one. At one time it had been a sign of madness to believe that the earth goes round the sun; to-day, to believe that the past is inalterable. He might be alone in holding that belief, and if alone, then a lunatic. But the thought of being a lunatic did not greatly trouble him: the horror was that he might also be wrong.” -George Orwell, Nineteen Eighty-four
Let me be clear about a few things up front before telling you how this seems to have happened and what’s going on with this ridiculous moment of academic history—for academic and academic-only it is. This, tedious and difficult to understand as it is, turns out to be centrally important to the present moment and this ridiculous episode, which is but a starkly clear microcosm of a far broader phenomenon by which academic disciplines are being colonized and conquered from within. I contend that this phenomenon represents a potentially existential risk to advanced modern civilizations, and, by the same actors insisting that two and two don’t necessarily make four, am being mocked for saying so. I now hope to convince you otherwise through several thousands of words no one ever should have had to write.
To elaborate, while the most popular assertion being made to counter “2+2=4” happens to be “2+2 can equal 5,” this coming from people including from self-described mathematicians and genuine math educators, among others, the Critical Social Justice activists’ point isn’t that 2+2=5 any more than it is that two and two represents any particular quantity. Their point is that 2+2 can equal 5, though it doesn’t have to. That is, their point is that the objectively true statement “2+2=4” can be deconstructed by means of claiming that it is possible that, in fact, other things can occur too. This allows them to sidestep accusations like that they’re denying that “2+2=4” even while they do it, and (we have to admit) fairly enough because their whole point has literally nothing to do with what two and two add to equal.
The activists’ point comes in three stages. First, it is that a statement like “2+2=4” is just one mathematical truth among many, and this seems to be a point that many mathematicians who should know far better are eager to help them make. Second, it is that “hegemonic narratives” don’t get to decide it objectively, and thus that nobody can say that “2+2=4” is objectively true, which is, of course, patently ridiculous. Third, it is that narratives that have been considered hegemonic in the past or present (e.g., “2+2=4”) should be regarded with extreme suspicion going forward into the future, and people who can make a claim to being oppressed by “hegemonic narratives” at all get to have the say on how we should think about those narratives and their specific contents, including simple matters of quantity. That is, the activists are seeking a radical rewriting of the entire rational project, and any reason that doesn’t forward their favored actors as the sole arbiters of what is true and correct needs to be deconstructed by rhetorical tricks and marginalized by moral and, perhaps, physical force and intimidation. They’re seeking a revolution.
This is meant to be accomplished via a distinctly postmodern approach that deliberately removes any sense of stable meaning to anything. In few examples could it be more stark than in the effort to argue that two and two aren’t necessarily four that the objective of the postmodernism at the heart of the present Critical Social Justice (or “Woke”) movement is to destabilize any sense of solidity and meaning and then to use the ensuing confusion to advance a particular form of radical politics.
Why is it so clear here? There’s no other reason to deny something so fundamental as “2+2=4” than to generate precisely this kind of confusion, and then into that confusion it is repeatedly asserted that “objectivity” in mathematics, even elementary arithmetic, is the kind of illusion that the powerful delude themselves and others into believing so that they can exclude other possibilities. This statement, of course, divorced from the specific context of what two and two add to equal is a remarkable political tool that could justify literally any double standard or abuse. The name for this approach to manipulating meaning is “deconstruction,” hence my use of this specific term so far, and as it arises explicitly from the poststructuralist ramblings of Jacques Derrida, its postmodern roots cannot reasonably be denied.
How Did This Happen?
“He picked up the children’s history book and looked at the portrait of Big Brother which formed its frontispiece. The hypnotic eyes gazed into his own. It was as though some huge force were pressing down upon you – something that penetrated inside your skull, battering against your brain, frightening you out of your beliefs, persuading you, almost, to deny the evidence of your senses.” -George Orwell, Nineteen Eighty-four
As strange as this turn of events is, the whole affair demands a proper account of how it came to be. The story actually starts in a private text dialogue with someone who was asking me specifically about how postmodernism thinks about objective claims about the world. She asked, at some point, what postmodernists would say about “2+2=4,” specifically asking me if postmodernists would say “2+2=5.” The answer, I told her, is no. The answer is “2+2=doesn’t matter, so long as what it equals isn’t constrained by hegemonic discourses.”
In some sense, the postmodern understanding is “2+2 can equal whatever people want it to equal, and we should be very skeptical of the idea that it equals 4 because so much political dominance is already built into that answer and how it is obtained.” To paraphrase a key point of Michel Foucault, the postmodernist avatar, whether or not a truth claim is actually true or false misses the point that a political process leads to making that determination. For the postmodernists, and their ideological descendants, it is only being radically skeptical of this political process that is of relevance, thus arriving at the formulation I gave. This is, of course, what the activists in the present case are doing, being radically skeptical of the alleged “politics” of mathematics when the whole program is viewed as a “cultural process.”
This particular radical effort, incidentally, is taken further by the new, more critical (as in, based in Critical Theory) ideology that has adopted postmodern tools, which would take the additional step of classifying a “hegemonic” solution as being indicative of some underlying systemic oppression, particularly exclusion of “other ways of knowing” (like “lived experience”) and “other knowledges” that might say otherwise. That is, in the conceptual operating system underlying Critical Social Justice (i.e., Woke) thought, 2+2 might sometimes equal 4, but we have to understand that accepting this as an objective statement of basic arithmetic contributes to a system of oppression that, in other corners of its existence, oppresses racial, gender, and sexual minorities, women, the overweight, the disabled, and people outside of the “Western context,” which is accused of accepting statements like “2+2=4” in an “uncritical” way (which means without using the favored Critical Theory of the relevant moment).
Pause to breathe. The activists behind this really think like this, and one of the weirder battles of the culture war of the day rages around that fact.
Anyway, to get back to the story, I proceeded to take this thought from my messages to the public in the form of a “Woke Mini,” a line of satirical quips roughly imitating dictionary entries with the goal of exposing and highlighting the inanity of the Critical Social Justice worldview. One of them is for the entry “2+2=4,” and it reads:
“2+2=4: A perspective in white, Western mathematics that marginalizes other possible values.”
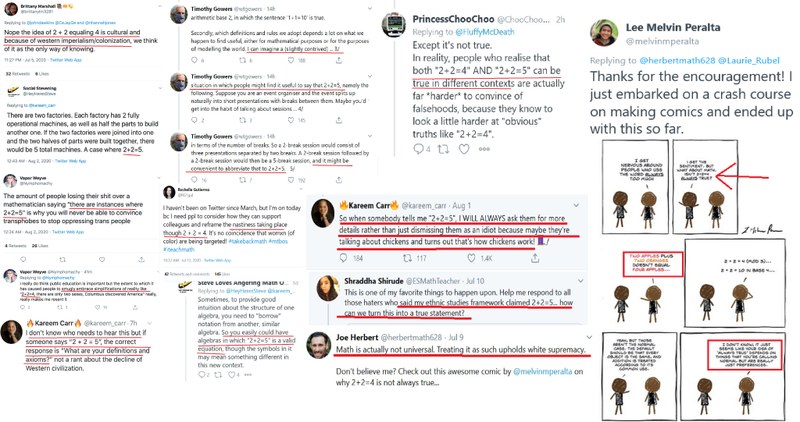
I tweeted that particular card for the first time on June 8 of this year, and, hopefully, you get the joke. It seemed humorous enough and made my point, so I was content with it, as were many of my followers. What I underestimated, however, was the fact that in cutting far too close to the bone, I had inadvertently introduced a conceptual virus into the Woke Matrix. What happened next is what led us to the present moment in the course of human history.
As it happens, it appears someone put this Woke Mini into the employ of satirically replying to Nikole Hannah-Jones on the fifth of July in response to her tweeting, “I wonder if folks always talking about ‘standards’ ever stop to consider that it’s their so-called standards that are the actual problem.” Hannah-Jones decided to make fun of me by quote-retweeting this delightful troll, including the image of the “2+2=4” Woke Mini, and adding the comment, “Using Arabic numerals to try to make a point about white, Western superiority is just so damn classic.”
For those who don’t realize it, Nikole Hannah-Jones is the architect behind the New York Times’ Pulitzer Prize winning critical historiography called the “1619 Project,” so she’s no small potatoes. It got some attention, not least from people who seem to have dedicated much of their spare time to hating me on the internet in a semi-professional capacity.
In fact, as many people who follow me regularly will know, I have a veritable cottage industry of petty, envious academics who follow me around on Twitter specifically to hate me and to try to discredit everything I do. So far as I can tell, it’s their only hobby, and they’re genuine enthusiasts. One of these, Michael J. Barany, of the Science Technology and Innovation Studies department (read: critical science studies) of the University of Edinburgh, who had previously tweeted (in January of 2019) “1+1=2 is a hegemonic discourse and don’t let anyone tell you otherwise,” replied to “enthusiastically co-sign” to Hannah-Jones’ attempted takedown of my too-on-the-nose satire. (You’ll notice that Barany couldn’t disagree with or refute my claim in the Woke Mini, as he had made the same claim himself some 18 months prior and drew attention to it, so he could only sign on to a problematization of the fact that I would dare expose this fact about the critical-theory mindset.)
Soon after, also on July 5, “teacher, scholar, social justice change agent” and Ph.D. student Brittany Marshall joined in, apparently not understanding that she was making my point for me. She insisted, “Nope, the idea of 2+2 equaling 4 is cultural and because of western imperialism/colonization, we think of it as the only way of knowing.” This, if you don’t know, is the actual Critical Social Justice view of a “hegemonic discourse” like standard mathematics (including elementary arithmetic). You’ll notice that it’s significantly different than the idea currently being rabidly defended by well-meaning obfuscators on social media and now beyond, who have unwittingly (we hope) adopted the roles of useful idiots, that mathematics just admits a wider range of ways of approaching questions than the basic axioms of number theory. The point really is to create a complete Critical Social Justice revolution in mathematics and mathematics education by undermining any stable sense of reason or meaning. As you can read from a leading scholar-activist in this endeavor, Rochelle Gutiérrez,
Much of what currently counts as scholarship in mathematics education assumes we will work within the given system or expand what we currently count as the status quo. Within mathematics education, we have convinced ourselves that “equity” is a strong enough agenda when maybe revolution should be the goal.
Who goes on to observe that the co-optation of useful idiots in the form of real mathematicians is a necessary part of her revolutionary project:
One thing that has been underscored from this attack is that we cannot create a revolution by ourselves; we need accomplices (not allies) in this work. That is, we need people who are willing to stand with us, around us, so that those who attack us will need to go through them (first). Having accomplices is different than having allies who support with solidarity, cheer loudly from the sidelines, or who safely stand on the sidewalk with their signs. Accomplices do what Delores Huerta called for when organizing for the rights of Chicano farmworkers: “Walk the street with us into history. Get off the sidewalk.” Mathematicians are one group who are showing some promise in the arena of being our accomplices.
She then quotes the following passage about what “accomplices” are expected to do before explaining a litany of ways that even by 2017 mathematicians had become “accomplices” in advancing this revolutionary work: betray their institutions and, presumably, their fields themselves, by leveraging support for the “liberation” (this means Critical Theory, specifically neo-Marxism, by definition, by the way) effort.
An accomplice as academic would seek ways to leverage resources and material support and/or betray their institution to further liberation struggles. An intellectual accomplice would strategize with, not for, and not be afraid to pick up a hammer. (Indigenous Action, 2014, p. 5)
Speaking of picking up a hammer to take to mathematics, and as a notable interlude in this already weird “2+2” affair, on July 10, an ethnic mathematics teacher and councilperson for the Washington state Ethnic Studies program, Shraddha Shirude, jumped in on the discussion after discovering someone saying something to the effect of adding two apples plus two oranges equals four pieces of fruit—as though the need to group by like units is at all mysterious—is an eye-opening way to challenge people who are rightly criticizing her ethnomathematics (yeah, that’s a word now) program. She wrote explicitly, “This is one of my favorite things to happen upon. Help me respond to all those haters who said my ethnic studies framework claimed 2+2=5… how can we turn this into a true statement?” And, so, the project to make “2+2=5” into a “true statement” began in earnest.
One would hope that the whole thing would have puffed up, been funny and terrifying for a week, and died from there, but such people underestimate two things: first, the fact that the Woke really do think this way and hate for normal people to be able to see it clearly, even though they say it themselves constantly, and second, because I am helping people see their game clearly for what it is, that I must be wrong, problematic, and, above all, discredited completely at all costs. Thus began a relentless attempt by a band of petty Crits to discredit me that has included a professional and academic defense of “2+2=5” that has been raging through the entire month of July 2020. Now, at the time of writing in early August, it seems to have begun to make the leap into the mainstream, necessitating this silly explanation.
What Are They Saying?
“In the end the Party would announce that two and two made five, and you would have to believe it. It was inevitable that they should make that claim sooner or later: the logic of their position demanded it. Not merely the validity of experience, but the very existence of external reality was tacitly denied by their philosophy.” -George Orwell, Nineteen Eighty-four
Although it’s generally true that no one wants to have to stomach more mathematics than they absolutely have to, looking at some of the actual ways these activists and their water-carriers have tried to defend that two and two aren’t necessarily four is obligatory so that the general themes of their activism can be exposed and explained. That theme is this: there is, in every case, some play on words or meaning in at least one of the basic concepts on the table: “two,” “five” or “four,” “plus,” and “equals.” That is, they’re playing word games with the pretense to being profound all with the underlying (and amusingly backfiring) motivation of getting more people to be willing to destabilize meaning and accept deconstruction so that they, the enlightened deconstructionists, can tell people what is right and wrong to think in any given circumstance. Oh, that and to make sure I’m wholly discredited, which is, as I’ve observed, basically some people’s favorite hobbyhorse.
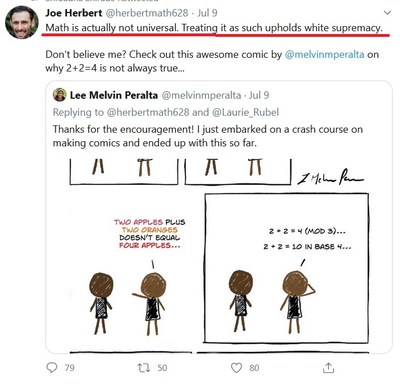
They’ve made an argument to inconsistent units. To paraphrase: You might say that two apples and two apples is four apples, but at the same time two apples plus two oranges equals four pieces of fruit shows that addition is contextual, and what constitutes the more universal unit is a socially constructed decision, and thus 2+2=4 is not universally true because sometimes it’s 2+2 (two and two) = 2+2 (two and two).
Explanation: This is more than a bit silly. In applied mathematics, there is no addition possible across unlike units. You cannot add an apple to an orange without reclassifying them both in the same terms, like as fruit. This is important in physical applications, say like describing the acceleration of an object, because acceleration only means anything in terms of how the rate of change of position changes in time (i.e., say, how does the speed in {meters per second} change per second). You can’t directly add an acceleration (with those units) to a velocity (with other units) because it doesn’t mean anything. Thus, addition requires similarity of units.
In pure mathematics, numbers are unitless, but the underlying assumption to that is that in being unitless, numbers have the same units, and if put to application, that condition must hold. You can only add “like” things together by the definition of “plus.” This seems to score a point for the “contextual” argument, except that it’s just playing a word game. Whether you call the apples and oranges “piece of fruit,” “generic biomatter,” “trash,” or “objects” is irrelevant, so long as they can both be described within that broader category, and the total quantity of whatever category you want to consider is still four, no matter how you slice or dice it. This is a willful application of a little trick, a word game. The point of the word game is to make that seem more mysterious than it is (not at all) for people who aren’t particularly mathematically savvy enough to understand that they’re being had.
They play this same word game in reverse too, intentionally, by employing a shift of numerical bases. To paraphrase: 2+2=4 in base-10 arithemetic, but in base-3 arithmetic, 2+2=11, not 4.
Explanation: This one is almost infuriating, and it’s a willful exploitation that most people take for granted that we’re working in the “common base” (ten) because that’s literally the point of a common base: everyone gets to take it for granted unless directly specified otherwise. Yet again, this is a stupid word game that they’re using to trick people.
To understand how it gets played, take note that it is no huge mystery to anyone with better than a first-grade education that “2+2=3+1” is mathematically true because both values are, in fact, still four, and four is four is four is four no matter how you write it down. This particular way to write four, “11 (in base 3),” means “3+1.” It is a form of shorthand for the way base-3 (ternary) arithmetic would write the value four. In plain English, which mathematical symbols represent, four is expressed this way in ternary: “a single three plus a single one equals four.” This isn’t mysterious at all. The mathematical expression “3+1” is, in fact, one 3 added to one 1, which can be rendered in base-3 (ternary) numbers as (2+2)_3=11_3 (one notation for indicating numerical bases is this, with the underscore or a subscript followed by the specified base).
Activists pulling this wool over your eyes conveniently don’t write the base explicitly and clearly. Instead, they write, “in base-3 numbers, 2+2=11, not 4.” The trick is that 11_3 (one, one, in base-3) means 4 as it is expressed in every numerical base above 4. It, 11_3, literally means 3+1 in exactly the same way that 253, in the common base (10), means two 100s plus five 10s plus 3 ones (mathematically: 1(200)+5(10)+3(1)). This is a shift in notation of exactly the same type as how “four” in English, “cuatro” in Spanish, and “sì” (四) in Mandarin Chinese all mean the same thing. Saying “in base-3, 2+2=11, not 4” is a pun on the symbols “11_3” (one, one, in base-3) and “4.” It’s just a word game, not a change in values, and it’s no more sophisticated than if they said 2+2 equals cuatro, not four, in Bolivia. This doesn’t disrupt objectivity in math, just in the notation one might choose to write it down.
They play this game by shifting to modular (or clock) arithmetic. To paraphrase: Imagine a clock with values 0, 1, and 2. If you start at 2 and then add 2 more, you go from 2 to 0, then to 1, so 2+2=1 on a clock with numbers 0, 1, and 2.
This, in abstract algebra (which I had never dreamed I’d have to write a popular essay about) is called “modular arithmetic,” and what the “clock” represents is what are known as “residue classes.” These are the possible remainders when you divide by a given number (in the given example, 3). That is, when you divide any number by 3, you end up with three possible remainders: 0 (divisible by 3), 1, or 2. As it turns out, the usual rules of arithmetic are more or less preserved onto the residue classes, and so you end up with “+” having a natural “modular” analogue when you shift from regular arithmetic to modular arithmetic. For example, 8+5=13, as we all know. If we look, though, 8 leaves a remainder of 2 when divided by 3; 5 also leaves a remainder of 2 when divided by 3; and 13 leaves a remainder of 1 when divided by 3. Thus, 8+5≡2+2≡1 (modulo 3), and 13≡1 (modulo 3), so 8+5≡1 (mod 3), as mathematicians might indicate it. This isn’t a mistake. Modular arithmetic works this way.
So, does 2+2=1 (mod 3) (emphasis on the equal)? No. It doesn’t. Both the “+” and the “=” are different in modular arithmetic, as are the meanings of the numbers themselves. That’s the word game. Notice that the binary relation in modular arithmetic is not “=” but instead “≡.” This is because modular arithmetic doesn’t provide equality but equivalence (in terms of residue/remainder classes when divided by the relevant base value). These aren’t the same “relation” (as they’re called). There’s also a difference in the “+,” as these residue classes, as a set, form a specific group together with modular addition as the operation. Modular addition is derived conceptually from the usual addition, rather clearly, but it isn’t the same binary operation and doesn’t even apply in the same mathematical structure. Further, the symbols 2 and 1 here are elements of the residue class of integers modulo 3, not the usual numbers, so they don’t even have their usual meaning. That means these activists are, again, playing a word game. Four, an integer, doesn’t change in value because the symbols “2+2” behave differently in a different mathematical universe.
Mathematicians are content to play fast and loose with the shorthand when the specific context (here, of the relevant group) is clear, but they would also specify that context and accept that without further specification, the common one of usual integers and usual addition, especially if the equals sign is employed, is to be assumed. If wanting to use modular arithmetic, they’d write something like, “in the group ℤ/3ℤ, 2+2≡1 (mod 3),” which indicates to any informed reader that none of the symbols in use are understood in their usual way. It’s an abuse of notation to do otherwise, and any mathematician who is obfuscating on this point knows it because this is junior-level undergraduate abstract algebra, not some way-out-there stuff.
One “former mathematician,” Kareem Carr, of Harvard, took this residue-class argument further, literally to the point of his own absurdity, to establish “2+2=5” explicitly. The thing is, “2+2≡5” isn’t true in any modular base except the trivial one, 1. In that trivial base, for the non-maths out there, what’s being asked is to classify all of the numbers by the remainder they leave when divided by 1. That remainder is always 0 because every integer is made out of the relevant sum of ones (that is, by definition, a number like 4 is 1+1+1+1). That means that the only residue class group in which 2+2≡5 (which still is not 2+2=5) is the one in which the only value is zero. In other words, in the relevant group, every number ≡ every other number, so 2+2≡5 (mod 1) doesn’t tell us anything at all. All Carr has managed to do is render an especially meaningless manipulation of symbols to prove a philosophical (not mathematical) point that one can play with words to say that sometimes two and two don’t look like they add to four.
But wait, you might insist! If these other mathematical groups (or what-have-you) exist, then 2+2 doesn’t have to be 4, and we do have other mathematical universes (if we will) in which the Crits are right. No. Again, the symbols “2,” “+,” and “4” mean something different in those contexts, and so this is no more profound than misusing a word that has two meanings in two different contexts except that the activists are doing it on purpose, counting on people not to understand it, so they can “expand potentialities of being” and politics, as Foucault would have it. The kindest thing that can be said of this game is that they’re confusing themselves (and others) specifically so they can win an argument on the internet.
From here, the entire “2+2=5 discourse” really started to get silly. Activists desperate to satisfy Shraddha Shirude’s demand to find a way to make “2+2=5” into “a true statement” employed a number of positively stupid tricks and manipulations.
To quote a few examples:
“There are two factories. Each factory has 2 fully operational machines, as well as half the parts to build another one. If the two factories were joined into one and the two halves of parts were built together, there would be 5 total machines. A case where 2+2=5.”
No, a case where 2.5+2.5=5, which everyone knows is true for the exact same reason that 2+2=4.
“Have you ever bought 2 and gotten the 3rd free? Or at least seen such an offer? price of 2 = price of 3. Buy 1 for $2, buy 3 for $4. 1 costs $2, but also 1 costs ~$1.33”
No, this is a case where the unit price is variable depending on the number purchased but addition is stable given that unit price.
“Literal-minded people might sometimes say things like I put a rooster and a hen together and I came back a year later and there were three of them (1+1=3) or they might say I left a fox and a hen together and later I came back and there was only one (1+1=1).” (Incidentally, this one is from Kareem Carr.)
No, here, 1+1 made 2, and then one of the ones either reproduced or was killed, resulting in another plus or minus 1. The arithmetic checks out the same as usual, and adding in this extra confusion about what “literal-minded people” would think doesn’t add clarity, only unnecessary confusion. This, by the way, was given in support of another statement by Carr: “Statements like ‘2+2=4’ are abstractions. What that means is they’re generalizations of ‘something’. You should always think of these statements as associated with an underlying reality. As a data analyst, I love numbers but it’s my job to connect them to reality.” (One hopes not this way, frankly.) Do note the explicit intention to redefine what a “reality” is. This is postmodernism, and it’s every bit as ridiculous as usual.
Another example in this vein: “2+2 doesn’t always equal 4. ‘2’ is a naming convention that aligns extremely accurately with 1000s of years of historical learning and synthesis that knows doubling it almost always equals ‘4’. It’s still not ‘always’ and ‘reality’.
I’m telling you; they really think this way. They believe that their words and the meanings of the symbols we use to communicate about it create different “realities,” and the “dominant and hegemonic discourses” unfairly marginalize and exclude alternatives like this nonsense.
Another “reality” that was presented (by Carr) was that if you are trying to get from point X to point Z through an intermediate point Y, and it’s $200 from X to Y and $200 from Y to Z but $500 from X to Z directly, then because you go from X to Z in both cases for $400 or $500, respectively, two (hundred dollars) plus two (hundred dollars) equals five (hundred dollars). But when you write it down this way, the “reality” falls apart. There are just two ways to get from X to Z, and one is cheaper than the other, and twice two hundred dollars is still four hundred dollars on the cheaper route. The usual arithmetic lets us understand what’s going on.
“Sometimes, when you put two grams of something with another two grams of something, you get five grams.” (Arthur Chu)
Nothing in the universe actually works this way, except words.
Several people developed the theme of imprecise measurement, however, in other ways, for example explaining that if your measuring instrument isn’t accurate enough, it might mark 2.3g as 2 and 4.6g as 5, thus, for that instrument, “2+2=5.” Carr himself levied such an example. The problem with this logic is that 2.3+2.3=4.6 is still the relevant, standard arithmetic, and they just need a better scale, a basic understanding of significant digits, and a little more general intelligence or personal integrity (or both).
Things got far worse than this too. To give you a sense of how profound the word games in this activist deconstruction project can be, consider this cleverly idiotic example:
“What if you wrote it as two+two=five [written vertically] [with] t=5, w=2, o=3, f=1, i=0, v=4, e=6. 523+523=1046”
For what it’s worth, the stunning example just above was sent to Shraddha Shirude in reply to her request to find a way to make “2+2=5” into a “true statement,” and she, a leader in Washington state’s Ethnic Studies education program, replied, “I love this.”
And finally, my favorite (so far),
“2+2=5 when the symbol ‘2’ refers to the value ‘2.5’, or more generally, when it refers to something that is equivalent to whatever ‘5’ refers to when operated on by ‘+’”
This last one one gives away the other half of the activist game (the word game part) so explicitly that it’s literally perfect. It’s a direct explanation that if you just change the meanings of the relevant symbols, you can use them to write something down with a different meaning, i.e., codes exist, and they seem to believe that everything is just a code, either for the right politics or the wrong. And this is what they do with everything else in our language too: “racism,” “anti-racism,” “black lives matter,” “rape culture,” “misogyny,” “critical,” “hate speech,” “diversity,” “inclusion,” “fascism,” and “anti-fascism,” being examples that might stand out particularly (though my favorites are “authenticity” and “engagement”). All it says is this utterly pointless triviality: If you change that which a symbol or sound signifies, it means something different. What a shock, then, how often these activists accuse everyone around them of talking in “coded language,” huh?
Objectivity in Mathematics
“The heresy of heresies was common sense. And what was terrifying was not that they would kill you for thinking otherwise, but that they might be right. For, after all, how do we know that two and two make four? Or that the force of gravity works? Or that the past is unchangeable? If both the past and the external world exist only in the mind, and if the mind itself is controllable—what then?” -George Orwell, Nineteen Eighty-four
This has, of course, been very tedious, and maybe few will have read this far, but it’s worth wrapping up with an attempt to defend the objectivity of mathematics and make sense of the tiny little trivial crack through which Critical Social Justice postmodernism is able to wedge all this nonsense.
Mathematics, in its greatest generality, is actually hard to define except in saying that it would be that branch of abstract inquiry that has somehow at its foundations axioms of numeracy. You might think that geometry, in dealing with shapes and forms, offers a counterexample to this, or if you’re more sophisticated that either topology or set theory does, but this, I think, is incorrect. Geometry gives away the game in its name: geo–metry, the measure of the Earth, and those measurements are relevant to what the field does, even if it doesn’t do it all the time. Topology, even if it were to use no numbers at all, nevertheless derives from explorations about the behaviors of objects called “open sets” first on the real number line or multidimensional real (or complex) space. So it goes with set theory as well, even if no set contains any numbers at all (indeed, one of the key concepts in set theory is “cardinality,” which is an abstract extension of the answer to the question “how many?”). Its usual fundamental axioms, the Zermelo-Fraenkel axioms, were a reformulation of the much more basic Peano axioms of earlier number theory, and other formulations extended from there.
Mathematics therefore derives from axioms, explored logically, and those axioms can either be explicit constructions (as, say, with the axioms of infinity or choice, which are suggested by abstract extensions of numbers themselves) or what seem to be self-evident truths about the world (such as, “there exists a number 0, the additive identity, such that 0+0=0”—if you have nothing, and you add nothing to it, you still have nothing). It is accurate to say that if we change the underlying axioms, or even the underlying logic that operates upon them, we would result in a different mathematics, and these things have been explored mathematically and philosophically, whether they correspond to the real world or not. (A simple analogy is to what the Tufts philosopher Dan Dennett called “chmess,” which are games based on chess but with some changes to the usual rules—games that many mathematicians and philosophers often like to play with, to produce statements of “no abiding significance,” as Dennett puts it.)
Mathematics is in that sense a form of philosophical inquiry where the underlying axioms, thus fundamental premises, are relatively uncontroversial for philosophical exploration. Usually, in fact, the core or base-level axioms (from which others are suggested) are also relatively simple and connect to the real world in a very obvious way, or did at one time and have been extended from there. For example, the numbers, so the fundamental axioms of set theory came from a reformulation of those of number theory, and those are very easily tied to real-world counting experiments. And experiments they are, at least at first: the basic operations like addition, subtraction, and multiplication can be verified in small-value cases empirically with literally no variation ever. Three rocks put together with seven rocks always results in ten rocks. This results in being able to define abstractions (axioms) about numerical and related subjects with very little ambiguity, and the mystery of why the resulting systems of truths describe the real world so well is only mysterious because we forgot where we started: with very simple, very obvious observations that admit absolutely no variation from one experiment to the next.
That is, the usual mathematics tends to start with genuinely self-evident truths (we call this “mathematical realism” although it can be done, as Bertrand Russell did at length, through “mathematical formalism” as well), and if we chose to start with different fundamental assumptions, we’d have a different mathematics that doesn’t seem remotely interested in reality at all (these are often explorations within “mathematical nominalism” that divorce mathematical objects from reality, and formalism can feed into this as well). The Critical Social Justice activists are uncritically appealing to mathematical nominalism (and subjectivism) without ever making a case for it, as though its mere existence as school of philosophical thought justifies its status as a destroyer of mathematical objectivity and the entire realist (and other schools) of mathematical philosophy. It’s hard to label this behavior with any friendly terms, so I’ll refrain, but I will say it seems to work on mathematicians who don’t know the full context of what’s going on in this debate.
Though it’s an aside, for an explanation of how this confusion could possibly be widespread enough to turn working mathematicians into Rochelle Gutiérrez’s “accomplices,” one needs to understand that most working mathematicians aren’t all that interested in the underlying philosophy of mathematics. This is for the simple reason that because they mostly have no need to be, as the philosophy of mathematics has very little to do with the actual doing of mathematics (isn’t this always the case?). This fact has been explained, however, by one who is, Ian Stewart. A sufficient explanation appears in his Letters to a Young Mathematician, where he wrote, “the working philosophy of most mathematicians is mostly an unexamined Platonist-Formalist hybrid.” There’s rarely a deep exploration, therefore, of what mathematics really is or what it means—realist, formalist, nominalist, objectivist, or subjectivist—on the part of mathematicians, which leaves them ripe for being made into unwitting “accomplices” in an idiots’ revolution. As it turns out, when one’s foundations are largely unexamined, postmodern rhetorical nonsense can pretty easily blow the person off them, and this seems even to be the case with the Fields Medal winner Timothy Gowers, who has unfortunately been dragged into this mess.
Regardless of what system one chooses, once we decide upon our axioms and an operant logic, we can then talk about the “axiomatic system” it generates as “a mathematics,” if we want. Statements within that axiomatic system fall into one of three categories: true, false, or indeterminable. In the usual axioms and logic of basic number theory, “2+2=4, in the integers, with the usual addition” is a provable statement that is completely true. “2+2=5, in the integers, with the usual addition” is a provably false statement that is completely untrue. “There are infinitely many integers” is an undecidable statement that requires the introduction or rejection of a new axiom to bring into existence (and not all mathematicians accept the axiom of infinity, saying instead things like “the quantity of integers is indefinite”). One could therefore think of the “mathematics” at hand as being the set of provably true statements in that axiomatic system and the project of doing mathematics as finding out what those are, something of a very difficult but very simple sorting question predicated upon truth values, and, however hard proofs, disproofs, or proofs of indeterminability may be in practice, there is no ambiguity in the status of any statement in the system whatsoever.
Here’s where the matter of “objectivity” comes into focus. Within the context of the axiomatic system at hand, a true statement (called a “theorem”) is completely true and absolutely in no sense false or indeterminable. You’ll notice I did not say it is “objectively” true because I don’t want it to get lost that “objectivity” means something more than merely being absolutely true within a specific context.
The phrase “objectively true” means the relevant statement also says something meaningful and accurate about the world outside of subjective experience—that is, it depends upon mathematical realism or at least a quasi-realism through formalism (often branded as “positivism” by the Woke, which they very much dislike). This is precisely what the postmodern effort is meant to break down, though, by rendering it seemingly absurd that we could know anything about the world outside of subjective experience, and it results in lots of double-meaning games played on “objective” happening in the Critical Social Justice analysis, most importantly including the insistence that it means “outside of human bias.” That’s not what “objective” in the relevant sense means, however.
Objectivity, in the relevant sense, means corresponding faithfully to reality, and thus mathematical statements can be considered objectively true to the degree that they faithfully represent reality. The basis of the postmodern question about objectivity is, is it possible to determine faithful correspondence to reality given that we’re imperfect instruments who necessarily are caught up in our own subjective experience? The postmodern reply to this question is an emphatic “no,” although the emphasis of that denial is, our own political biases make it impossible to trust any claim on objectivity, so it is those political biases that are of interest. That is, postmodernism is, in some sense, the complete politicization of everything knowable, including the claims to knowledge themselves and the epistemologies used to make those claims. The fact that they can send messages to this effect over the internet, however, is an effective, if not philosophically complete, practical refutation of their philosophy.
Speaking as a realist, reality doesn’t care about any of this immensely human confusion, of course, and so absolutely nothing is changed about basic facts like that—no matter what else—if I am called upon to lift up four rocks two at a time, I will end up doing the lifting action exactly two times to complete the task, leaving no remainder. Further, if I push together two pairs of cherry tomatoes, the result will be four cherry tomatoes, not five, every time (no matter how you slice them). This unambiguously means that four is twice two, or two twos put together in succession, which can be written down in mathematical shorthand as “2+2=4” or “(2+2)_3=11_3,” if we have cause to use ternary numbers instead of the standard decimal digits. That shorthand carries all sorts of information about what is meant by the symbols involved, but the meanings of those symbols are not ambiguous in their common expression and should be clearly articulated anytime it is not (as with switching to ternary).
A mathematical statement of elementary arithmetic like “2+2=4” is therefore, in fact, objectively true (even the water-carrying accomplices agree). The relevant meanings of the terms (“2,” “+,” “4,” and “=”) are stable and unambiguous to the precise degree that it is reasonable to accept that common, and not alternative, meanings can be assumed unless otherwise stated. This, though, is the very definition of “reasonable,” which is the precise definition postmodern epistemology seeks to undermine as being prima facie absurd.
Of course, other statements using these or similar symbols with different meanings do not represent a deviation from this objective truth and may provide another truth (e.g., that on a rotating “clock” with values 0, 1, and 2, adding 2 turns of the hand twice takes you around once and back to 1). They also may not (e.g., that one rooster plus one hen plus one successfully hatched chick somehow is the same thing as 1+1=3). What determines the difference is also not arbitrary, “contextual,” or cultural but rather the same simple qualification: the alternative is objectively true if, and only if, that statement also corresponds faithfully to reality (“faithfully” fails in the chicken example).
Don’t Be an Accomplice
“But no! His courage seemed suddenly to stiffen of its own accord. The face of O’Brien, not called up by any obvious association, had floated into his mind. He knew, with more certainty than before, that O’Brien was on his side. He was writing the diary for O’Brien – to O’Brien: it was like an interminable letter which no one would ever read, but which was addressed to a particular person and took its colour from that fact.
“The Party told you to reject the evidence of your eyes and ears. It was their final, most essential command. His heart sank as he thought of the enormous power arrayed against him, the ease with which any Party intellectual would overthrow him in debate, the subtle arguments which he would not be able to understand, much less answer. And yet he was in the right! They were wrong and he was right. The obvious, the silly, and the true had got to be defended. Truisms are true, hold on to that! The solid world exists, its laws do not change. Stones are hard, water is wet, objects unsupported fall towards the earth’s centre.” -George Orwell, Nineteen Eighty-four
The common meanings of mathematical symbols like “2,” “+,” “4,” and “=” are also not arbitrarily chosen. They have arisen not out of the abstract ether or any particular cultural context but from the bare fact of reality that once we define a quantifier “1” to represent the quantity of a single object of a given (perhaps broad) description, 1 and 1 make 2 and 2 and 2 make 4, by definition. “Four,” as a quantity, no matter how it is represented, literally means 1+1+1+1 in that system of thought, and that system corresponds to reality perfectly faithfully. The only “cultural” processes involved on any level are which cultures happened to be first (Indians and, by way of India, Golden Age Arabian Muslims) to use particular grunts and squiggles to mean the things that we take to be the values two and four, the binary operation plus, and the binary relation equals, and which cultures currently use them (basically all of them). That has no impact whatsoever on the basic fact that all of these have clear, unambiguous meanings that are ultimately derived from simple observations of facts about reality that are true in every conceivable cultural setting (at least in this universe).
This means that “2+2=4,” once the symbols being used are explained in the context they are intended, is objectively true and cannot be false. By the same token, “2+2=5” is objectively false and cannot be true. The only way in which this can be changed is by changing the underlying definitions of the symbols themselves, which means by engaging in a fallacy of equivocation that could be resolved—rather, exposed—merely by offering full transparency on what each symbol means. (This might remind the reader of “trans women are trans women,” which, despite being a tautology, is a higher resolution statement than “trans women are women,” which is a word game being played disingenuously with the word “woman,” which represents a particular kind of category that can be defined, clearly, in more than one way.) By means only of this mere equivocation, mathematicians and others are being made into “accomplices” in a revolution they, I would dare guarantee, would not otherwise support.
So, now I’ve written well over 8000 words on the stupidest topic I could possibly have imagined ever having to write about, but it matters—and there’s a point to take away from all this. It is that postmodernism, particularly in the hands of the ideology of Critical Social Justice, is not at all interested in truth. It is only interested in power, which it will establish through its attempted revolution, which it in turn knows it can only achieve by turning otherwise intelligent, well-meaning people into “accomplices” by manipulating their good will, charity, fear of being disliked or ostracized, and, especially, unawareness of what is actually going on beneath the rhetorical tricks they’re being served up with intentionally limited context.
To achieve this revolution, postmodernist Critical Social justice is centrally interested in destabilizing meaning so that those it anoints as sufficiently virtuous can decide what is “true” and so that no one has any grounds upon which they could disagree, even in principle. It is a direct assault on reason itself by means of destabilizing the meaning of meaning with the purpose of installing its own priestly caste of arbiters of how things will be according to the rubrics it lays out. This is, however, as I claimed at the beginning, a breakdown of the fundamental logic of civilization, which depends entirely on the ability for each citizen to generally understand something of how that civilization operates. It is also a replacement of that fundamental logic of civilization with the fundamental logic of something more basic and less able to meet the needs of the people who will still be forced to live within it: self-interest, cronyism, corruption, and an unstable form of uncivilized might-makes-right that will surely eventually collapse into the more brutal and familiar stable sort in which whomever can kill enough people gets to make the rules.
“Freedom is the freedom to say that 2+2=4. If that is granted, all else follows” -George Orwell, Nineteen Eighty-four
Maybe don’t be an accomplice, then.
References:




